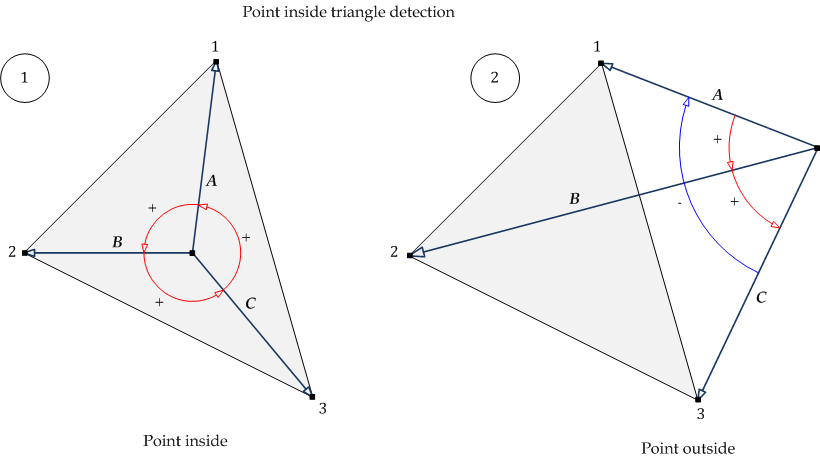
The
following table shows some analogy between electrical and fluid systems. It is
useful for people who want to understand one of these systems by comparing with
another system. Also, it’s pretty useful for hydraulic circuit designers as
they may get ideas from existing electronic circuits and apply it to hydraulics.
|
Electrical
|
Hydraulic
|
|
Electric current
intensity (Ampere = Coulomb\sec)
|
Mass flow rate
(kg\sec)
|
|
Electric potential
difference (voltage difference)
|
Pressure gradient (difference)
|
|
Electric charge
quantity
|
Fluid mass
|
|
Flexible wire
|
Flexible hose
|
|
PCB (Printed Circuit
Board)
|
Rigid pipes
|
|
Diode
|
Check valve (one-way
valve)
|
|
Electric capacitor
|
Elevated tank or
accumulator
|
|
Triger diode DIAC
|
Pressure regulator
valve
|
|
Battery
|
Pump
|
|
On /off switch
|
Valve
fully-opened/fulley-closed
|
|
Electric resistance
|
Pipe friction,
entrance and exit losses, and fittings losses.
|
|
Potentiometer (variable
resistance)
|
Proportional valve
|
|
Fuse
|
|
|
Step down
transformer: Reduces voltage and increases current intensity
|
Nozzle: Increases velocity and
reduces pressure
|
|
Step up transformer:
Increases voltage and decreases current intensity
|
Diffuser: Decreases
velocity and increases pressure
|
|
Inductance: Shows
some impedance when electric current changes and has zero impedance when
current is fixed
|
Rotary motor: Shows
some impedance when mass flow rate changes (due to rotor inertia).
|
|
AC current
|
Pulsating flow
|
|
Dielectric insulator
|
Seal
|
|
Reference →
Earth (ground)
|
Reference → Free
surface (atmospheric pressure)
|
|
Comparator
|
Differential valve
|
|
Logic gate OR
|
OR (shuttle) valve
|
|
Relay
|
Hydraulic-actuated
valve
|
|
Optocoupler
|
Hydraulic coupling
|
|
Electric surge
|
Water hammer
|
|
Eddy current
|
Turbulent flow
|
|
KCL
|
Continuity equation
|
|
KVL
|
Bernoulli equation
|
|
Ameter
|
Flow meter
|
|
Voltameter
|
Pressure gauge
|
|
Medium: electric
conductor
|
Medium: fluid
|
|
Electric resistivity
|
Fluid viscosity
|
|
Circuit breaker
|
Isolation valve
|
|
Amplifier
|
Hydraulic
intensifier
|
|
Bundle cables
|
Laminar flow element
|