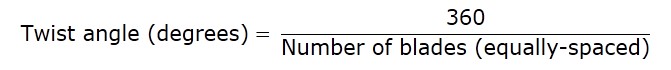Assume that
you are using a painting/diagraming software and you’ve created certain shape
(in our example it is just a square). Also, assume that you want to array this
shape for 100 times in one row and the software does not support arraying. So,
what are you going to do in this case? Are you going to draw the shape for another
99 times? Or are you going to copy the drawn shape and paste it 99 times? Or what?
I thought
about this problem and found that I can copy the original shape and paste it x
times to create a group of shapes, then I’m going to copy the group and paste
it y times to get the final array. Consider the following example and
figure in which we want to create an array of 10 squares. There are many
solutions like the following:
|
Solution
|
Number of copy-paste/redrawing operations after drawing the
original shape
|
|
Draw the square 10
times
|
9
|
|
Draw the square
once, copy once, and paste it 9 times
|
9
|
|
Draw the square
once, copy it, and paste it once. Now, you have a group of two squares; copy
the group and paste it 4 times (1)
|
5
|
|
Draw the square
once, copy it, and paste it twice. Now, you have a group of three squares;
copy the group and paste it 2 times. Finally, copy the square and paste it
once. (2)
|
5
|
|
Draw the square
once, copy it, and paste it 3 times. Now, you have a group of four squares;
copy the group and paste it once. Finally, copy the square and paste it twice.
(3)
|
6
|
|
Draw the square
once, copy it, and paste it 4 times. Now, you have a group of five squares;
copy the group and paste it once. (4)
|
5
|
So, given
those solutions, what is the optimum or minimum time consuming solution. This is
the aim of this post. This method can be used for both linear and circular
arrays. As we noticed in the previous table that there may be many optimum
solutions. In the previous example the minimum number possible of operations is
five.
The following relation governs the copy and pasting by groups
To find the
best size of the group (number of elements in one group) we should calculate
the number of operations for each value ranging from 1 to the half of array
size. For extremely large arrays, you may need to construct the group itself
using this method.
At the end,
I want to say some thing … I’m using Microsoft Office Visio as the
drawing/diagraming software and it –in fact- supports two dimensional arraying,
but I used this method before I have knew that it does.
The other
thing I want to say is that I think that this method is going to be very useful
for those who want to create a helical Savonius blade die using discrete (very
thin) elements. In this case, you should know blade’s height and specify the
thickness of the element and so you get number of elements by division of the
previous values.