In this post I show a bug in blogger image encoder. When uploading images with white color background, the white color is displayed as light grey for some image extensions. I tested these images on Google chrome and internet explorer and does not seem a problem of the browser.The following are some tests for different image extensions.
Labels
- Computational Science (21)
- Mechanical Engineering (85)
- Misc. (48)
- PowerPoint (1)
- Scilab (15)
- VBA Programming (25)
Monday, February 24, 2014
Selection of measuring devices
The following points are helpful when selecting most of measuring devices:
Storage conditions:
Storage temperature and humidity
Working conditions:
Ambient temperature range
Humidity range
Sensitivity:
The minimum unit | step of measurement
Maximum measurement value
Auto-range or manual range:
Auto-range is preferred for non-professionals and for time saving
Resolution:
The number of right digits that can be displayed
Display | Screen type:
- Mon-color
- 7 segment or 15 segment display
- Dot matrix display
- Color display
Display | screen size:
The dimensions of screen
Display graph
Measuring units:
Different measuring units save the time of unit conversion
Response time | Stabilization time:
Time needed to reach the true value.
Hardware overload protection
Accuracy:
Tolerance of measurement +/- as an absolute value of a percentage of full scale reading. How much far the measured value from the actual value.
Precision | Repeat-ability:
How often the reading is repeated or how near the measured values.
Linearity:
How the electric signal is varying with the measure physical property. The higher the linearity, the lower number of points needed for calibration.
Sampling time:
The frequency of updating measurements
Recording/logging
Internal memory size:
Internal memory size for storing measured values
Power source:
- Direct AC current (internal adapter).
- Voltage range and frequency
- AC current with adapter
- Internal battery:
- Battery life
- Maximum battery on time
- Internally-recharged
- Externally recharged
On-screen battery indicator
Ruggedness:
The maximum drop distance after which the device malfunctions or is destroyed
Auto-power off time
Portability
Calibration:
-Has traced calibration certificate from NIST
-Can be calibrated: offsets can be saved in the device
Computer interface connection:
- RS 232
- USB
- HDMI
- Wireless
Computer software
- Device configuration from PC
PC-Online reading | recording
Open channel/not connected probes | sensors detection
Wrong probes | sensors connection detection:
This function is useful in multiple-function measuring devices
Replaceable overload protection
Device sealing | Keypad sealing
Device mounting options:
- Adjustable legs
- Magnetic -mount
- Screw mount
External Vs. internal sensor
Taring | Zeroing
Hold manual Vs. Automatic
Minimum, maximum, average
Counting:
This feature is available in tachometers, and balances
Programmable limit alarm
Buzzer sound quality
Probe length
Probe dimensions
Storage conditions:
Storage temperature and humidity
Working conditions:
Ambient temperature range
Humidity range
Sensitivity:
The minimum unit | step of measurement
Maximum measurement value
Auto-range or manual range:
Auto-range is preferred for non-professionals and for time saving
Resolution:
The number of right digits that can be displayed
Display | Screen type:
- Mon-color
- 7 segment or 15 segment display
- Dot matrix display
- Color display
Display | screen size:
The dimensions of screen
Display graph
Measuring units:
Different measuring units save the time of unit conversion
Response time | Stabilization time:
Time needed to reach the true value.
Hardware overload protection
Accuracy:
Tolerance of measurement +/- as an absolute value of a percentage of full scale reading. How much far the measured value from the actual value.
Precision | Repeat-ability:
How often the reading is repeated or how near the measured values.
Linearity:
How the electric signal is varying with the measure physical property. The higher the linearity, the lower number of points needed for calibration.
Sampling time:
The frequency of updating measurements
Recording/logging
Internal memory size:
Internal memory size for storing measured values
Power source:
- Direct AC current (internal adapter).
- Voltage range and frequency
- AC current with adapter
- Internal battery:
- Battery life
- Maximum battery on time
- Internally-recharged
- Externally recharged
On-screen battery indicator
Ruggedness:
The maximum drop distance after which the device malfunctions or is destroyed
Auto-power off time
Portability
Calibration:
-Has traced calibration certificate from NIST
-Can be calibrated: offsets can be saved in the device
Computer interface connection:
- RS 232
- USB
- HDMI
- Wireless
Computer software
- Device configuration from PC
PC-Online reading | recording
Open channel/not connected probes | sensors detection
Wrong probes | sensors connection detection:
This function is useful in multiple-function measuring devices
Replaceable overload protection
Device sealing | Keypad sealing
Device mounting options:
- Adjustable legs
- Magnetic -mount
- Screw mount
External Vs. internal sensor
Taring | Zeroing
Hold manual Vs. Automatic
Minimum, maximum, average
Counting:
This feature is available in tachometers, and balances
Programmable limit alarm
Buzzer sound quality
Probe length
Probe dimensions
Sunday, February 23, 2014
Cold appliances/Refrigerators/Freezer test analysis Excel add-in
For domestic (house-hold) refrigerators, refrigerators-freezers, and freezers being tested according to the standards IEC 62552, ISO 15502, or ANSI/AHAM HRF-1-2004; I have developed an Excel add-in that help in analyzing test data recorded by data acquisition system (temperatures, pressures, electric current, voltage, power, power factor, energy consumption).
What is really good in this add-in that it can be helpful for any laboratory/test engineer regardless the software used in acquisition. The add-in is programmed based on the field experience. It also can work with any number of temperature or pressure measurements. No matter how large the measurements record is large.
The add-in has two versions: one for Microsoft Excel 2007 and the other for Microsoft Excel 2010 as it is has the standard office ribbon control. It is programmed in native VBA code and user forms. It is interactive and may be used with any number of files opened in Excel. The add-in is still under development (error-proofing, error messages, and documentation), but here you are some snapshots of the basic general tool-boxes in it.
The standard ribbon interface:
Sensor compliance check:
Gap/overlap analysis:
Virtual channel analysis:
Compressor cycle analyzer:
Defrosting thermostat analysis:
Defrosting heating system analysis:
Pull-down times:
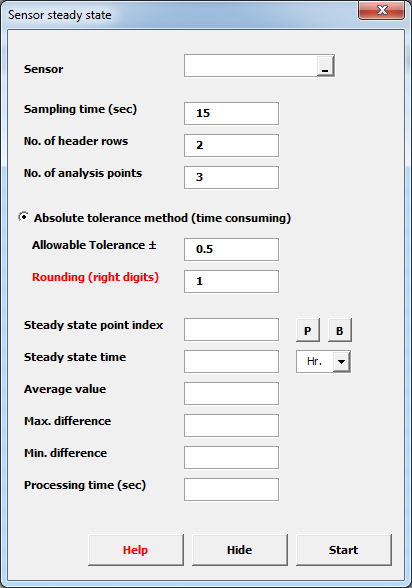
Pull-down steady state detection:
Compressor startability test analysis:
Test summary:
What is really good in this add-in that it can be helpful for any laboratory/test engineer regardless the software used in acquisition. The add-in is programmed based on the field experience. It also can work with any number of temperature or pressure measurements. No matter how large the measurements record is large.
The add-in has two versions: one for Microsoft Excel 2007 and the other for Microsoft Excel 2010 as it is has the standard office ribbon control. It is programmed in native VBA code and user forms. It is interactive and may be used with any number of files opened in Excel. The add-in is still under development (error-proofing, error messages, and documentation), but here you are some snapshots of the basic general tool-boxes in it.
The standard ribbon interface:
Sensor compliance check:
Gap/overlap analysis:
Virtual channel analysis:
Compressor cycle analyzer:
Defrosting thermostat analysis:
Defrosting heating system analysis:
Pull-down times:
Pull-down steady state detection:
Compressor startability test analysis:
Test summary:
Thursday, February 6, 2014
Detecting local minimum and maximum points
In this post, I introduce a new method to detect local minimum and local maximum points for a curve drawn by a discrete set of points. That means we don't have a mathematical formula for the curve and as a result we can't calculate local minimum and maximum points by differentiation to detect points of zero slope. I needed this method to detect local minimum and maximum points for a series of points (more than 30000 points) that are recorded by data acquisition system (temperatures).
If noise is exist in values and the points don't seem to form a single continuous mathematical function (more than function, so the local maximum and minimum points may be sharp vertices), then this method is highly recommended, but with some improvements needed.
The method simply is to divide the domain into relatively large number of divisions and detect the global maximum and global minimum of each division. The method looks like the bisection method for solving equations by iteration.
From one side, the global maximum in the division should be compared with the values at the start and the end of the interval. If the global maximum is not on the interval boundaries (larger than boundary points) , then it is a local maximum. The same concept applies for the detection of the local minimum. If the local minimum is not on the interval boundaries (lower than boundary points), then it is a local minimum.
The following illustrative figure (which is not my case) is for a friction-damped vibrating mass-spring system (Coulomb dry friction model) showing the displacement of mass versus time.
The white points show the boundary points of intervals, the green points show the local maximum points, and the blue points show the local minimum points.
For sure, some divisions will not contain local minimum or maximum points, while some will contain. Theoretically, number of divisions should be higher than the number of local minimum and maximum points.
One of the draw backs of this method is when the local maximum or minimum point is coincident with one of the interval boundaries (see the red point). This drawback can be solved by iterating with different number of subdivisions and check if there is any change or not (looks like the boundary conditions analysis in CFD). Also, it can be solved by shifting the boundaries of divisions with small amount and re-apply the method again.
Another draw back is when there are more than one point having the same maximum value.
Update:
In case of a curve that is cycling around an average value; a smart way to detect number of divisions is to calculate the average of the curve, then the interval boundaries are composed of the following points:
- Start point of the curve
- Intersection points of average line (reference line) with the curve
- End point of the curve
The following figure shows the implementation of automatic detection of number of divisions. The reference line may not be the average value, but may also be a user-input value.
If noise is exist in values and the points don't seem to form a single continuous mathematical function (more than function, so the local maximum and minimum points may be sharp vertices), then this method is highly recommended, but with some improvements needed.
The method simply is to divide the domain into relatively large number of divisions and detect the global maximum and global minimum of each division. The method looks like the bisection method for solving equations by iteration.
From one side, the global maximum in the division should be compared with the values at the start and the end of the interval. If the global maximum is not on the interval boundaries (larger than boundary points) , then it is a local maximum. The same concept applies for the detection of the local minimum. If the local minimum is not on the interval boundaries (lower than boundary points), then it is a local minimum.
The following illustrative figure (which is not my case) is for a friction-damped vibrating mass-spring system (Coulomb dry friction model) showing the displacement of mass versus time.
The white points show the boundary points of intervals, the green points show the local maximum points, and the blue points show the local minimum points.
For sure, some divisions will not contain local minimum or maximum points, while some will contain. Theoretically, number of divisions should be higher than the number of local minimum and maximum points.
One of the draw backs of this method is when the local maximum or minimum point is coincident with one of the interval boundaries (see the red point). This drawback can be solved by iterating with different number of subdivisions and check if there is any change or not (looks like the boundary conditions analysis in CFD). Also, it can be solved by shifting the boundaries of divisions with small amount and re-apply the method again.
Another draw back is when there are more than one point having the same maximum value.
Update:
In case of a curve that is cycling around an average value; a smart way to detect number of divisions is to calculate the average of the curve, then the interval boundaries are composed of the following points:
- Start point of the curve
- Intersection points of average line (reference line) with the curve
- End point of the curve
The following figure shows the implementation of automatic detection of number of divisions. The reference line may not be the average value, but may also be a user-input value.
Subscribe to:
Posts (Atom)